Signals & Systems Review-CH1

Signals and Systems Review - CH1

1.1 概述

信息.消息.信号

例子：电信号传递声音、图像、文字

信号是消息的表现形式，消息是信号的具体内容

系统

包括变换器、处理器等

$\Leftrightarrow$网络$\Leftrightarrow$电路

信号分析

目的：揭示信号特性及其改变方式

思想：分解成简单基本单元信号

系统分析

对指定输入激励的输出响应

1.2 信号描述

确定性信号&随机信号

确定性信号：对于指定的某一时刻t，可确定一相应的函数值f(t)，若干不连续点除外

连续信号&离散信号

连续时间信号：自变量的取值范围是连续的（实数域），用t表示连续时间变量

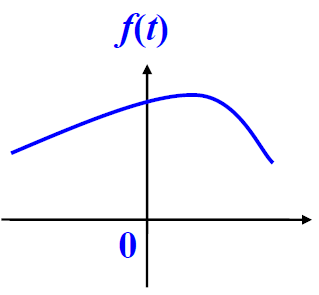
离散时间信号：自变量只取整数值的信号，用n表示离散时间变量

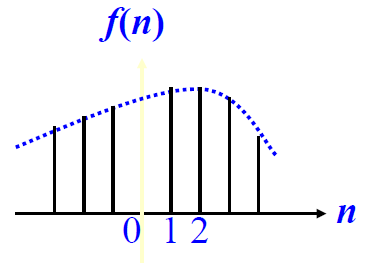
周期信号&非周期信号

周期信号：满足$x(t+T)=x(t)\space or\space x(n+N)=x(n)$

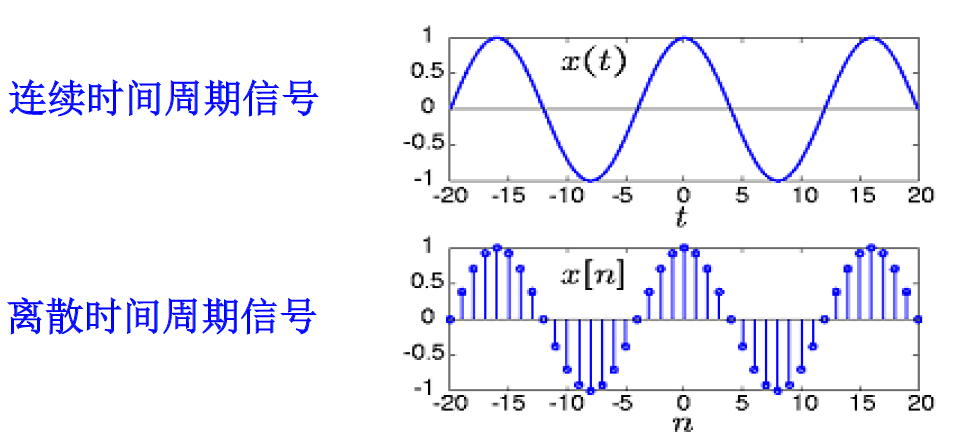
模拟、量化、抽样

模拟信号：时间和幅值均连续

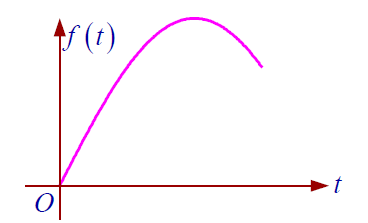
抽样信号：时间离散，幅值连续

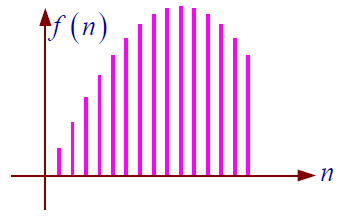
数字信号：时间和幅值均为离散

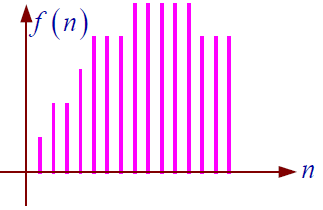
【模拟】$\rightarrow$抽样$\rightarrow$【抽样】$\rightarrow$量化$\rightarrow$【数字】

时间离散性$\Rightarrow$连续、离散

幅度离散型$\Rightarrow$(离散)抽样、数字

能量信号&功率信号

周期信号为功率信号，通常用它的平均功率来表征；

非周期信号可能为能量信号，也可能为功率信号，与函数形式有关。

典型确定性信号

指数信号

$$f(t)=e^{\alpha t}$$

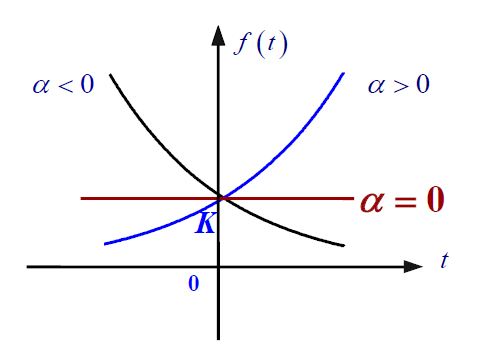
单边指数信号

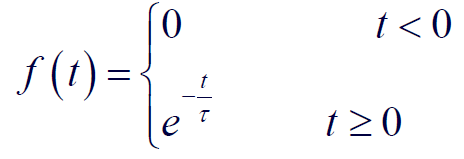
时间常数：$\tau = \frac{1}{|\alpha|}$，量纲为时间，代表衰减速度

重要特性：积分、微分仍是指数形式

复指数信号

$$f(t)=Ke^{st}$$

其中$s=\sigma + j\omega$为复数，称为复频率

$$f(t)=Ke^{\sigma t}cos(\omega t)+jKe^{\sigma t}sin{\omega t}$$

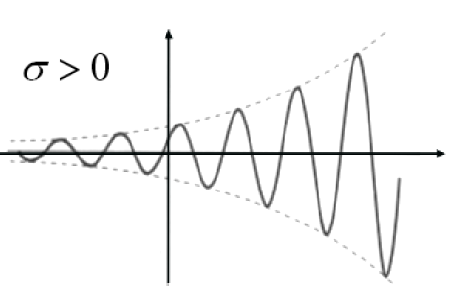
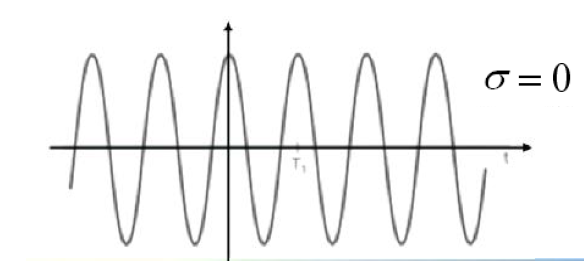
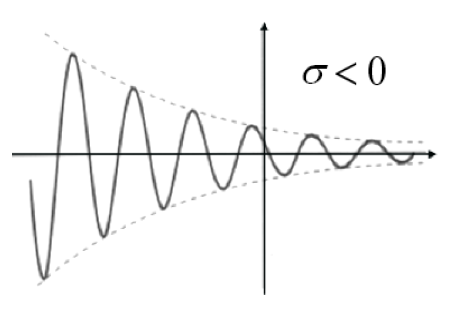
抽样信号

$$Sa(t)=\frac{sin t}{t}$$

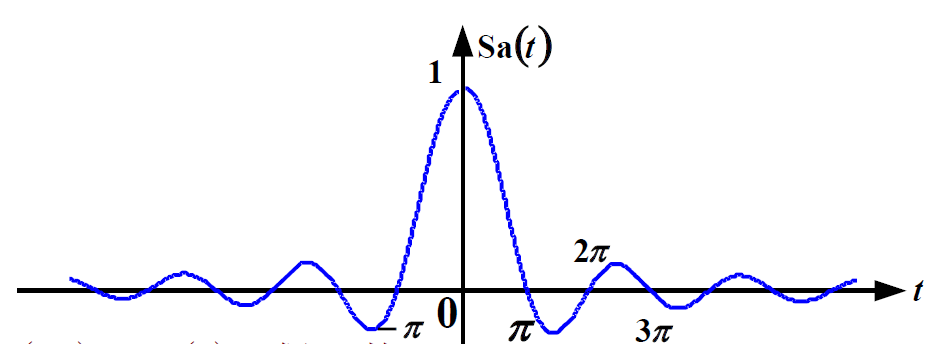
性质：

$$Sa(t)=Sa(-t)\space (偶函数)\\ lim_{t\rightarrow0}Sa(t)=1 \\ lim_{t\rightarrow \pm \infty}Sa(t)=0 \space(正负无穷都满足)\\ Sa(\pm n\pi)=0\space,n=1,2,3,...(没有0！注意！) \\ \int_0^{\infty}Sa(t)dt=\frac{\pi}{2} \\$$

sinc函数

$$sinc(t)=\frac{sin(\pi t)}{\pi t}$$

钟形信号(高斯函数)

$$f(t)=Ee^{-(\frac{t}{\tau})^2}$$

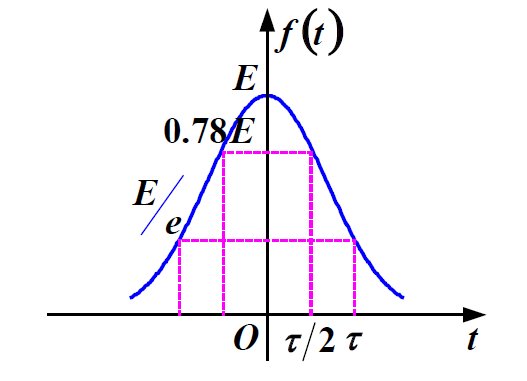
1.3 信号运算

宗量

宗量：可以理解为广义的自变量。这里的“广义”是指：自变量突破高中数学中的限制，可以是狭义的自变量，可以是函数，也可以是代数式……

可以依据宗量相同，函数值相同，求新坐标（！！！！）

移位

f(t)沿着t轴平移$\tau$得到

$$f(t)\rightarrow f(t-\tau) \\ \tau>0，右移（滞后） \\ \tau<0，左移（超前）$$

可以依据宗量相同，函数值相同，求新坐标

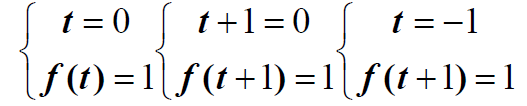
反褶

$$f(t)\rightarrow f(-t)$$

以纵轴为轴折叠，把信号的过去与未来对调。

没有可实现此功能的实际器件。

数字信号处理中可以实现此概念，例如堆栈中的“后进先出”。

尺度

$$f(t)\rightarrow f(at)$$

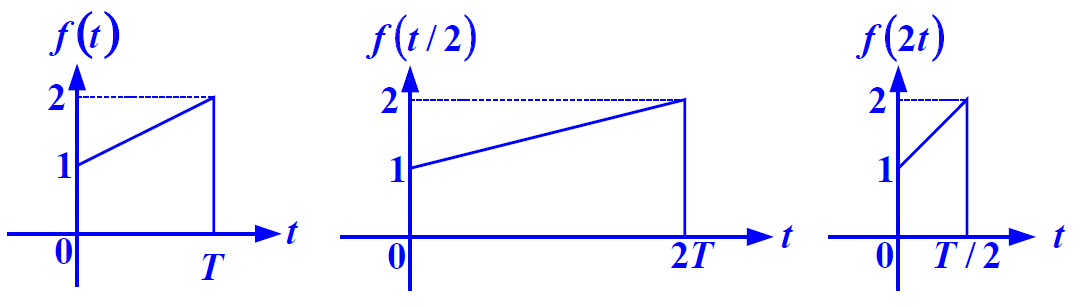
一般情况

$$f(t)\rightarrow f(at\pm b)=f(a(t\pm \frac{b}{a})) \space (a,b>0)$$

Steps:

1.尺度：a>1，压缩a倍；a<1，扩展1/a倍

2.移位：+，左移b/a；-，右移b/a

3.反褶：

$$f(a(t+\frac{b}{a}))\rightarrow f(-a(t+\frac{b}{a}))=f(-at- b)$$

1.平移量t0是自变量t净增减的量，即以f(t-t0)为标准形式来确定t0

2.反转时以被变换的宗量$\lambda=0$( 可以是t的复合函数）的直线为轴，即以f(-$\lambda$)为标准形式确定反转轴

3.尺度变换应以被变换的宗量$\lambda=0$(的直线为展缩中心线，即以f(a $\lambda$)为标准形式确定展缩中心线