降维观测器

降维观测器简介

引入

对于系统

$$\dot{x}=Ax+Bu \\ y=Cx$$

假设其中x的维数为n，y的维数为m。

全维观测器对全部变量x进行重构。但是如果状态的某些线性组合可以直接作为输出被测量出来(这由矩阵C决定)，就不需要进行估计，则可以降低其维数，仅需要额外获得n-m个维度的信息，之后配合观测得到的m个维度的信息，通过线性组合，就可以获得状态x的信息，由此引入降维观测器。

若C矩阵秩为m，则只需要重构余下的n-m个状态分量。

定义

给定线性系统$\sum(A,B,C):$

$$\dot{x}=Ax+Bu \\ y=Cx$$

其中C为$m\times n$矩阵，假定$rank(C)=m$，则一定存在线性变换

$$\overline{x}=Tx,where\space T=[D\space C]^T$$

其中D为使得$T^{-1}$存在的任意$(n-m)\times n$阵。

通过这一线性变换，系统变换为：

$$\dot{\overline{x} }=TAT^{-1}\overline{x}+TBu \\ y=CT^{-1}\overline{x}=[0\space I_m][\overline{x}_1\space \overline{x}_2]^T=\overline{x}_2$$

其中$\overline{x}_2$为m维，可以直接量测，因此只需要观测$(n-m)$维状态变量$\overline{x}_1$。

设计

为避免输出量的微分，重新定义观测器的状态

$$令W=\hat{x}_1+M_1\dot{y} \\ =(A_{11}+M_1A_{21})w+(B_1+M_1B_2)u+ \\ (A_{12}+M_1A{22}-(A_{11}+M_1A_{21})M_1)y \\ =(A_{11}+M_1A_{21})w+B_0u+Ey \\ 其中 \\ B_0=B_1+M_1B_2 \\ E=A_{12}+M_1A_{22}-(A_{11}+M_1A_{21})M_1 \\$$

上述称为Luenberger观测器。

由此得到原系统的状态重构：

$$\hat{x}=\left[ \matrix{ \hat{x} \\ y \\ } \right]=\left[ \matrix{ w-M_1 y \\ y \\ }\right]=\left[ \matrix{ I \\ 0 \\ }\right]w+\left[ \matrix{ -M_1 \\ I \\ }\right]y$$

误差分析

降维观测器的测量值y通过$M_1$直接反映在状态$\hat{x}_1$上，如图所示：

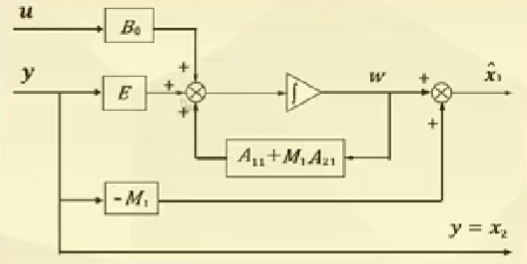
这样会将测量噪声带入，使得$M_1$的误差直接影响到$\hat{x}_1$稳态值，在全维观测器中则不存在这种误差。