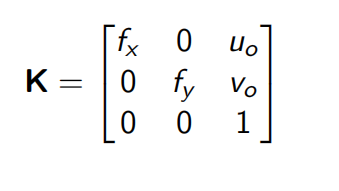IPMV lecture3 Perspective Transformation

03. Perspective Transformation

Preliminaries

范数

$l_p$-Norm (p范数)

$$||a||_p=(\sum_{k=1}^n |a_k|^p)^\frac{1}{p}$$

Infinity Norm (无穷范数)

$$||a||_{+\infty}=\max_i |x_i| \\ ||a||_{-\infty}=\min_i |x_i|$$

证明：令

$$a_{max}=max(|x_1|,|x_2|,...,|x_n|) \\ \Rightarrow ||a||_p=a_{max}(\sum_{k=1}^n (\frac{|a_k|}{a_{max}})^p)^\frac{1}{p}$$

又

$$1\leq \sum_{k=1}^n(\frac{|a_k|}{a_{max}})^p\leq n \\ \Rightarrow 1^{\frac{1}{p}}\leq (\sum_{k=1}^n(\frac{|a_k|}{a_{max}})^p)^{\frac{1}{p}}\leq n^{\frac{1}{p}}$$

根据夹逼定理(Squeeze Theorem)

$$\lim_{p\rightarrow\infty}||a||_p=\lim_{p\rightarrow\infty} a_{max}(\sum_{k=1}^n (\frac{|a_k|}{a_{max}})^p)^\frac{1}{p}=a_{max}$$

Q.E.D.

斜对称矩阵(skew-symmetric matrix)

定义

如果一个矩阵A是方阵，并且满足

$$A^T=-A$$

则为斜对称矩阵。

例如：

$$a=\left[ \matrix{ a_1 \\ a_2 \\ a_3 } \right]$$

的斜对称矩阵为

$$[a]_X=\left[ \matrix{ 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 } \right]$$

性质

1.基于定义

$$[a]_X=-[a]_X^T$$

2.消消乐性质(自己和自己的外积=0)

$$a^T[a]_X=0^T \\ [a]_Xa=0$$

3.叉积

$$a\crossproduct b=[a]_Xb=-[b]_Xa$$

4.【还不会证明】

$$det([a]_X^T)=(-1)^n det{[a]_X}$$

旋转矩阵

形式

沿着三根轴旋转的旋转矩阵依次为

$$[R]_\theta=\left[ \matrix{ cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 } \right]$$ $$[R]_\phi=\left[ \matrix{ 1 & 0 & 0 \\ 0 & cos\phi & sin\phi \\ 0 & -sin\phi & cos\phi } \right]$$ $$[R]_\Phi=\left[ \matrix{ -sin\Phi & 0 & cos\Phi \\ 0 & 1 & 0 \\ cos\Phi & 0 & sin\Phi } \right]$$

性质

$$RR^T=I \\ R^TR=I \\ |det(R)|=1$$

所有旋转矩阵组成的群称为特殊正交群(special orthogonal group, SO3)

矩阵运算

说明

以下讨论中标量(scalar)表示：

$$x$$

向量(Vector)表示：

$$y=[y_1,y_2,...,y_m]^T$$

矩阵(Matrix)表示(懒，没有手打)：

各种求导的表示：

【待填坑】

WCS vs. CCS

WCS(World Coordinate System)可以位于任何位置

CCS(Camera Coordinate System)必须设置在相机光心

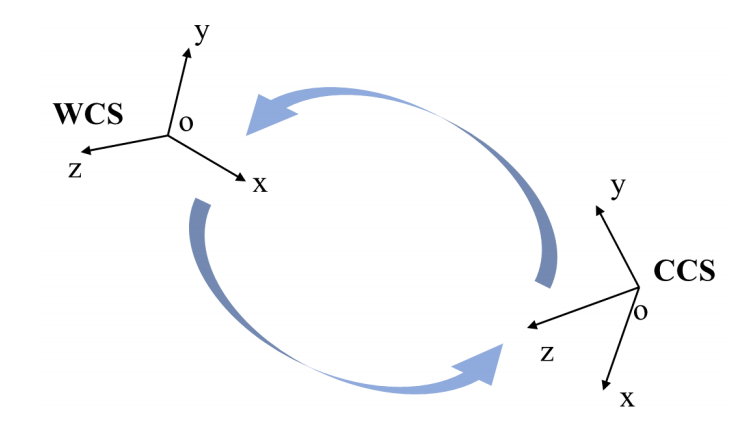
变换关系：

$$p_i^C=Rp_i^W+t$$

齐次坐标形式：

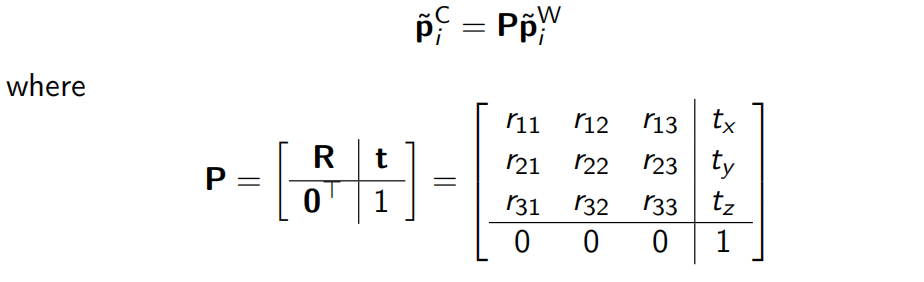
special Euclidean group(SE3): The group containing all homogeneous transformation matrices.

Pinhole camera model

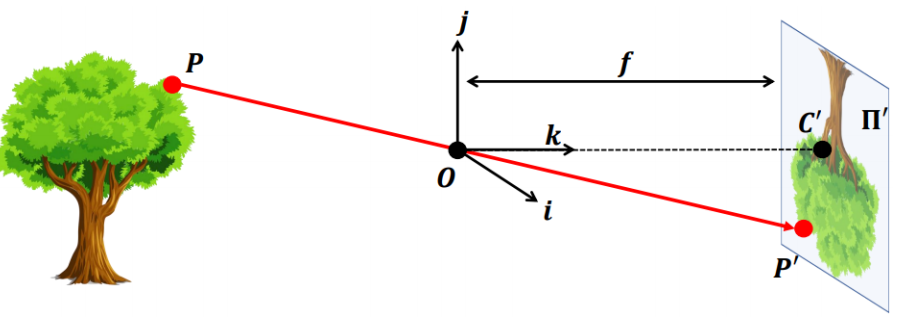
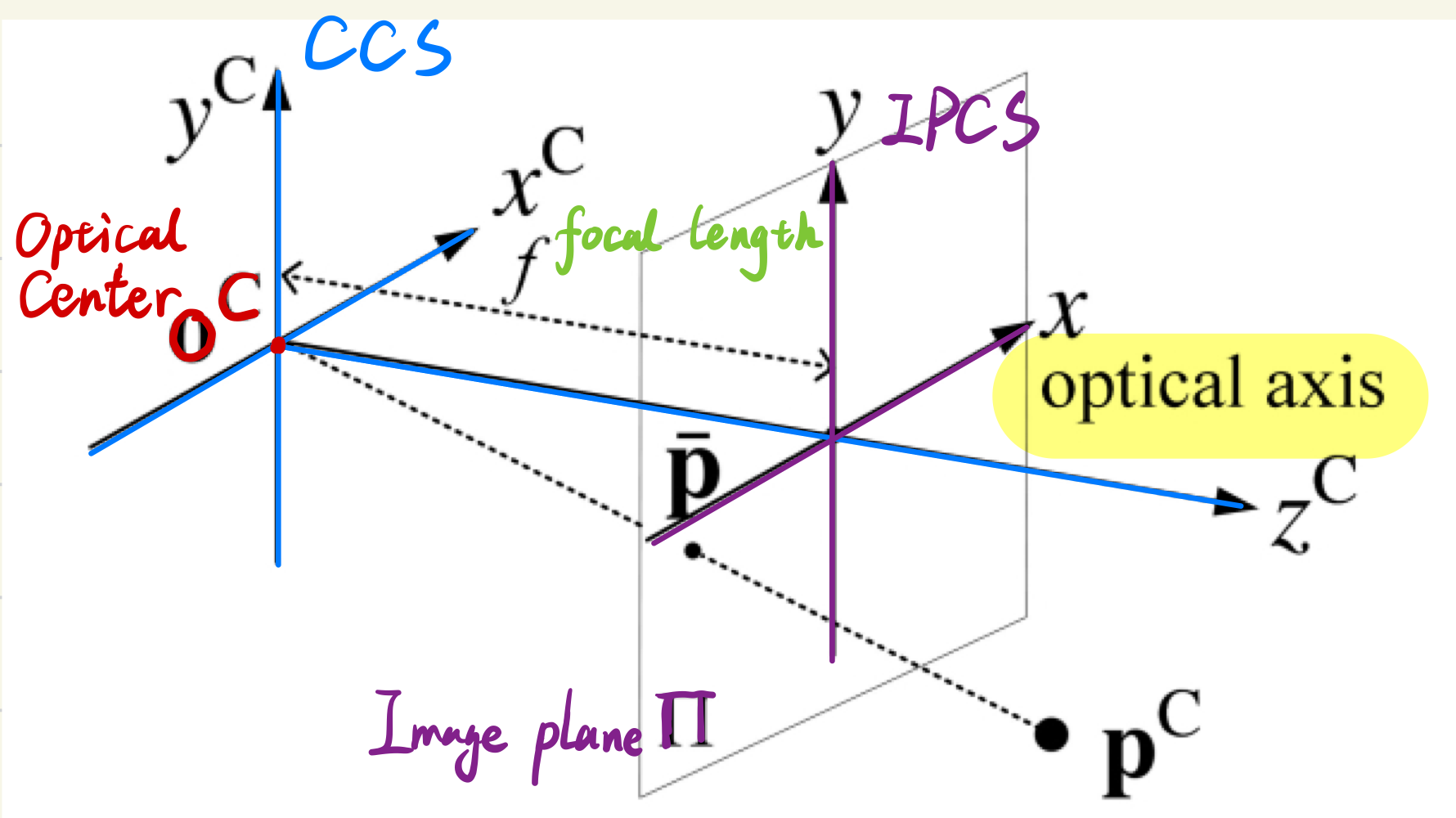
IPCS系中的坐标

$$\overline{p}=[x_i,y_i,f]^T$$

重要关系

$$\overline{p}=f\widehat{p}^C=\frac{f}{z_i^C}p^C$$

其中

$$\widehat{p}^C=[\frac{x_i^C}{z_i^C},\frac{y_i^C}{z_i^C},1]^T$$

是$p^C$的归一化表示(normalized).

Intrinsic matrix

意义：连接image plane coordinate system && pixel coordinate system

$$IPCS(x,y)\leftrightarrow PCS(u,v)$$

Lens distortion does not exist in a perspective camera model.

变换关系

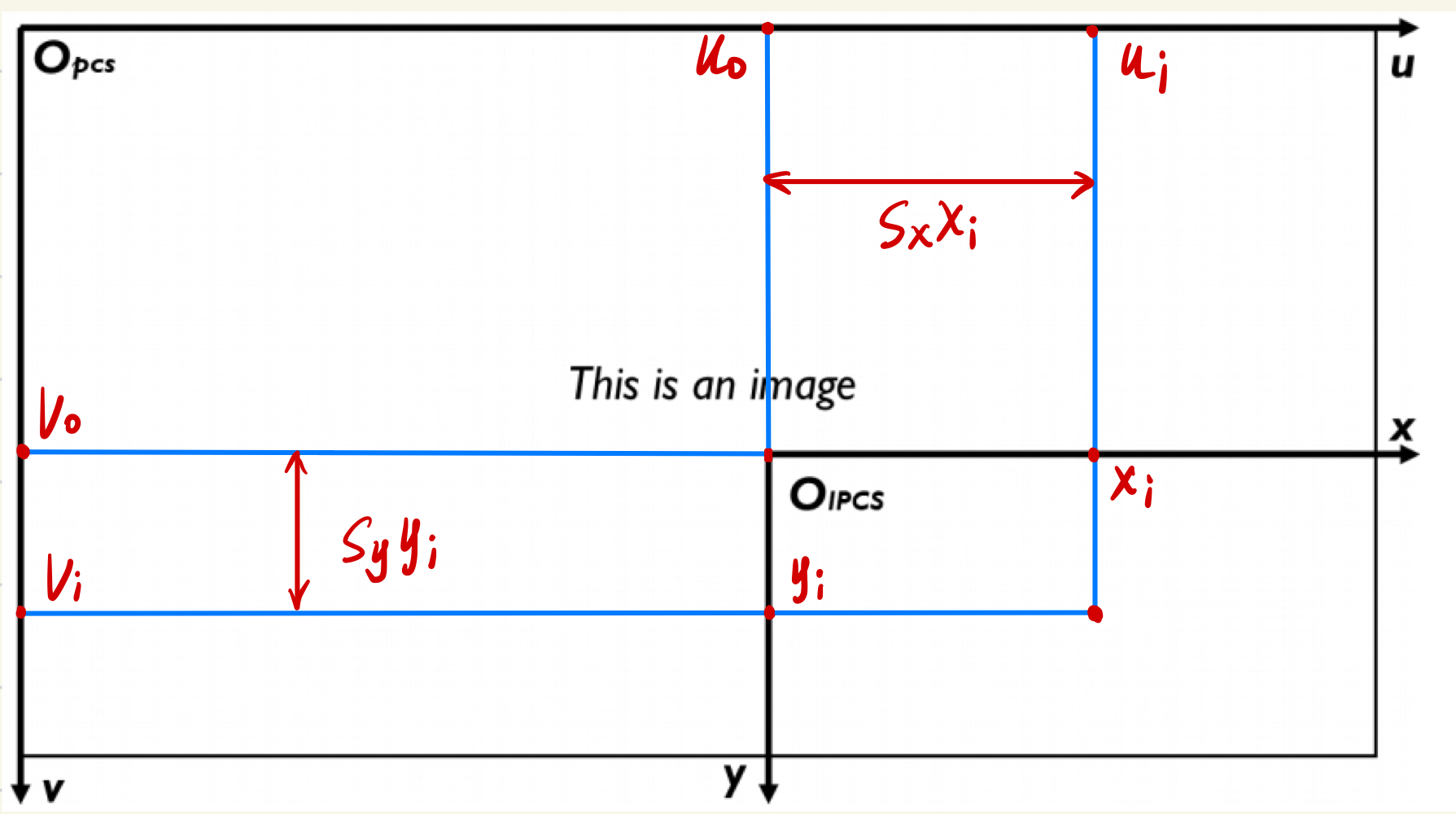
引入

$s_x,s_y$:effective size measured (in pixels per millimeter) in the horizontal and vertical directions, respectively.

$$f_x=fs_x \\ f_y=fs_y \\ x_i=f\frac{x_i^C}{z_i^C} \\ y_i=f\frac{y_i^C}{z_i^C}$$

可得

$$u_i=u_o+s_x x_i \\ v_i=v_o+s_y y_i$$

最终表达式

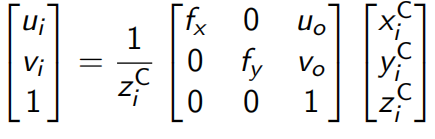
或表达为

$$\widetilde{p}=\frac{1}{z_i^C}Kp^C$$

说明：

1.$\widetilde{p}=[u_i,v_i,1]^T$是$p=[u_i,v_i]^T$的齐次坐标

2.intrinsic parameters:$u_o,v_o,f,s_x,s_y$

3.Intrinsic Matrix