Kalman Filter

Kalman滤波算法简介

基本介绍

卡尔曼滤波（也称为线性二次型估计），是一种最优化自回归数据处理算法，它的主要功能是：从一系列不完全且包含噪声的数据测量值序列中，估计出动态系统的状态。由于其效率高且所占空间较小，在雷达、计算机视觉、机器人导航等很多工程应用领域中都有应用。

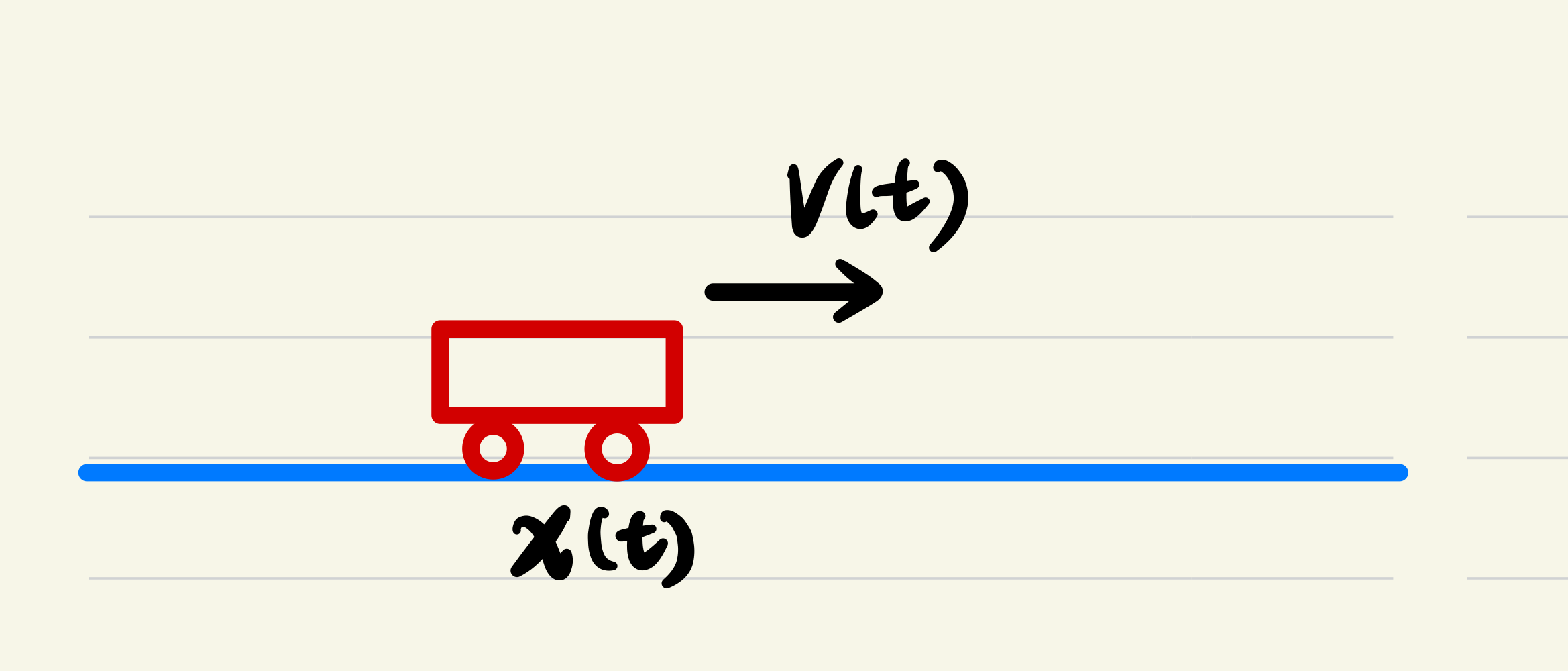
卡尔曼滤波的一个典型实例是：现在有一组有限时间内、包含噪声的数据，记录了物体运动中若干时刻的位置和速度，通过卡尔曼滤波算法可以根据这些数据预测出物体不同时刻的位置以及速度。

约定及说明

适用性

卡尔曼滤波适合于线性系统，且要求误差满足高斯分布。

状态空间表达式

本文中状态空间方程定义如下：

状态方程

$$x_k=Ax_{k-1}+Bu_k+w_k$$

表示了由上一状态到当前状态的转移关系。其中$x_k$表示当前时刻状态量，$u_k$表示当前时刻输入量，A,B均为系数矩阵，$w_k$为过程噪声(即真实的运动与理论方程所不相符的部分)。

观测方程

$$y_k=Cx_k+v_k$$

表示了当前时刻观测量的计算方式。其中$y_k$表示当前时刻的观测量，C为系数矩阵，$x_k$含义不变，$v_k$表示观测噪声(即由于观测仪器引起的噪声，如传感器带来的误差波动)。

参数说明

上述噪声$w_k$和$v_k$均符合高斯分布，为高斯白噪声，即

$$w_k \sim N(0;Q_k) \\ v_k \sim N(0;R_k)$$

约定：

$$\hat{x}_{k}代表最优估计值 \\ \hat{x}_{k}^-先验估计值(预测值) \\ x_k观测值$$

算法理解

宏观理解

卡尔曼滤波算法的实现过程是：使用上一次的最优结果（即先验估计值）预测当前的值，同时使用观测值（如通过传感器获得的数据）修正当前值，得到最优结果。

图解：

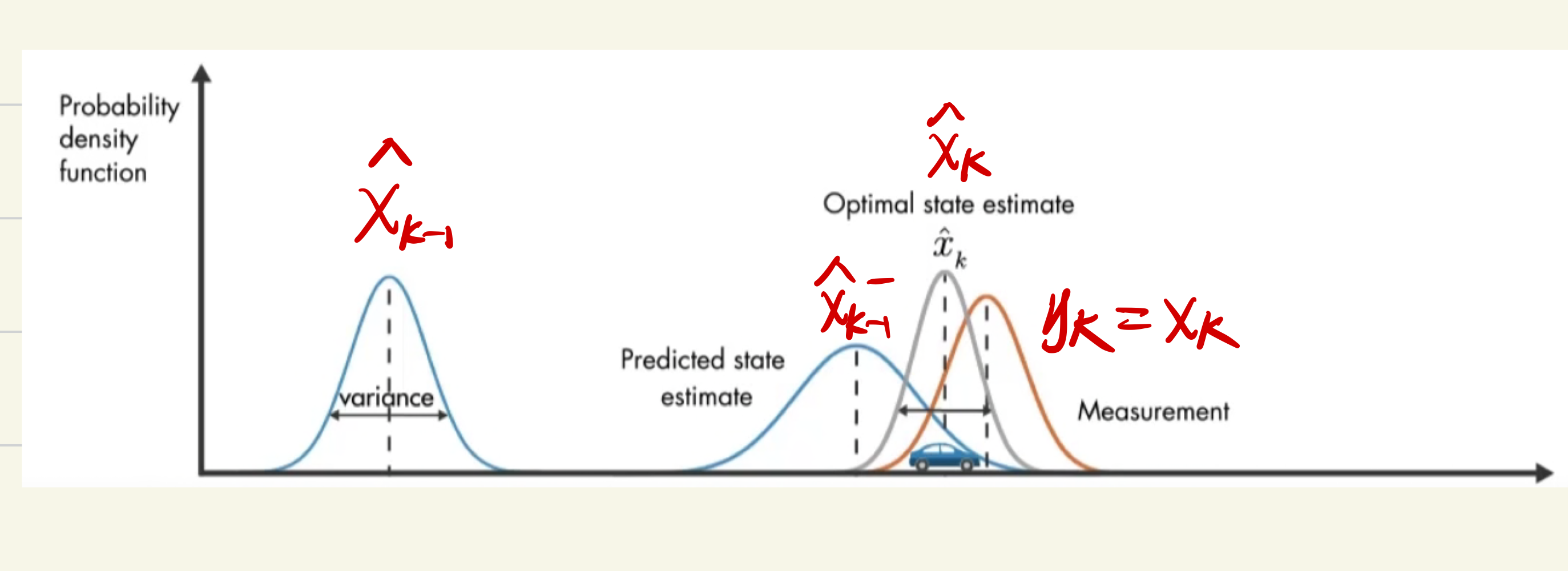
具体公式

本部分先逐个介绍各个公式的含义，最后再统一说明他们之间的关系。

预测部分

先验估计

$$\hat{x}_t^- = F\hat{x-1} + Bu_{t-1}$$

仍考虑第一部分中提到的小车的例子，假定小车做匀加速直线运动：

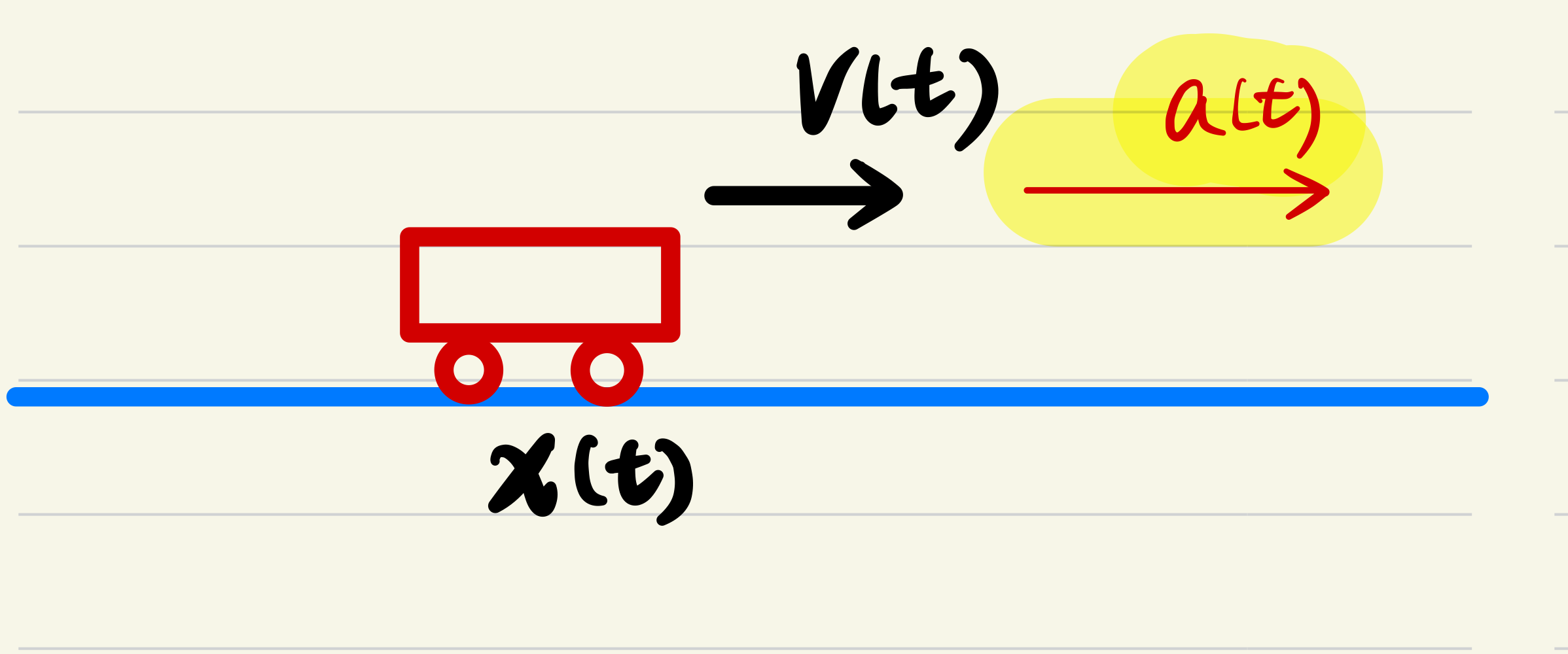预测模型可以写成

$$P_i=P_{i-1}+v_{i-1}\Delta t+\frac{a}{2}\Delta t^2 \\ v_i=v_{i-1}+a\Delta t$$

写成矩阵形式为

$$\left[ \matrix{ p_i \\ v_i } \right] = \left[ \matrix{ 1 & \Delta t \\ 0 & 1 } \right] \left[ \matrix{ p_{i-1} \\ v_{i-1} } \right]+ \left[ \matrix{ \frac{1}{2}\Delta t^2 \\ \Delta t } \right]a_i$$

则已经化成了上面先验估计方程的形式。

先验估计协方差

$$P_t^-=FP_{t-1}F^T+Q$$

可根据先验估计方程推导，如下：

$$根据协方差计算公式： \\ cov(Ax+k,Ax+k)=Acov(x,x)A^T \\ 先验过程中补上过程噪声：\\ \hat{x}_t^-=F\hat{x}_{t-1}+Bu_{t-1}+w_t \\ \begin{align*} \Rightarrow P_t^- &=cov(\hat{x}_t^-,\hat{x}_t^-) \\ &= cov(F\hat{x}_{t-1}+Bu_{t-1}+w_t,F\hat{x}_{t-1}+Bu_{t-1}+w_t) \\ &= Fcov(\hat{x}_{t-1},\hat{x}_{t-1})F^T+cov(w_t,w_t) \\ &= FP_{t-1}F^T+Q \end{align*}$$

测量方程

$$z_t=Hx_t+V$$

沿用上面小车的例子，这里的测量方程可以写为

$$z_P=P_t+\Delta P_t \\ z_v=0 \\ \Rightarrow \left[ \matrix{ z_P \\ z_v } \right] = \left[ \matrix{ 1 & 0 } \right] \left[ \matrix{ p_t \\ v_t } \right]+ \left[ \matrix{ 1 & 0 } \right] \left[ \matrix{ \Delta p_t \\ \Delta v_t } \right]$$

注意：$z_t$的维数未必与$\hat{x}_t$相同

状态更新部分

修正估计

$$\hat{x}_t=\hat{x}_t^-+K_t(z_t-H\hat{x}_t^-)$$

可以根据需求调整$K_t$的大小（如：更信任观测值还是估计值）

卡尔曼增益

$$K_t=\frac{P_t^-H^T}{HP_t^-H^T+R}$$

一维情况下(F=1,H=1)可以化简为

$$K_t=\frac{P_{t-1}+Q}{P_{t-1}+Q+R}$$

更新后验估计协方差

$$P_t=(I-K_tH)P_t^-$$

关系图

信号流图（转载）

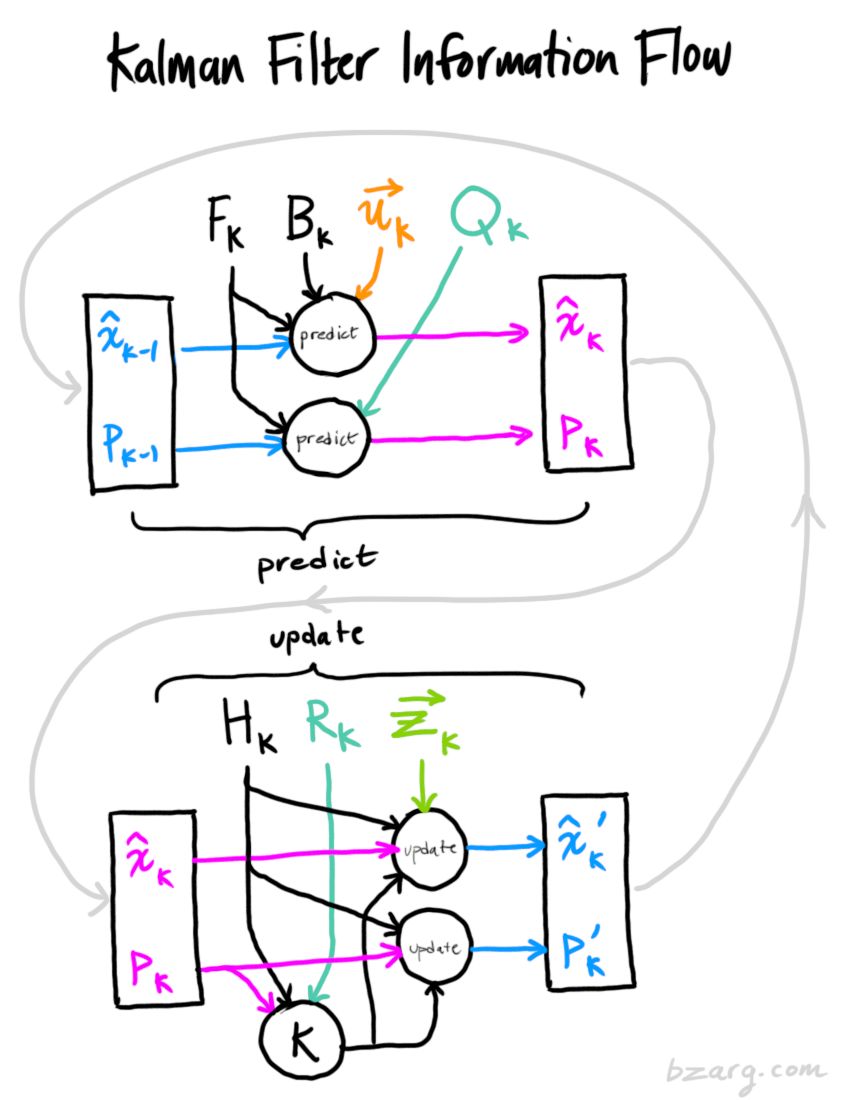
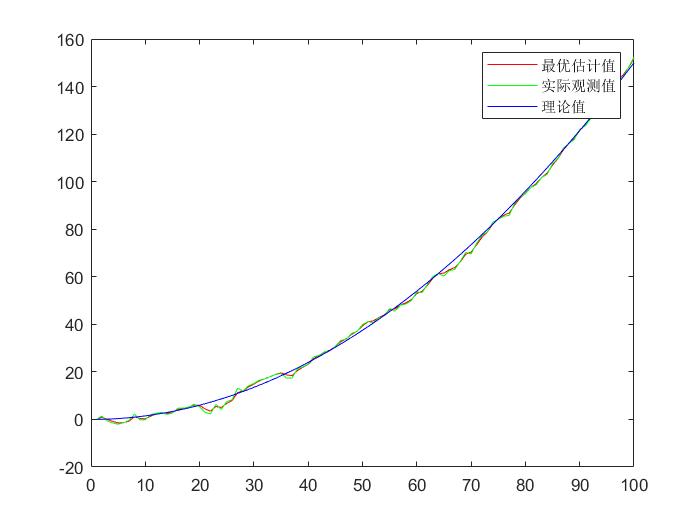
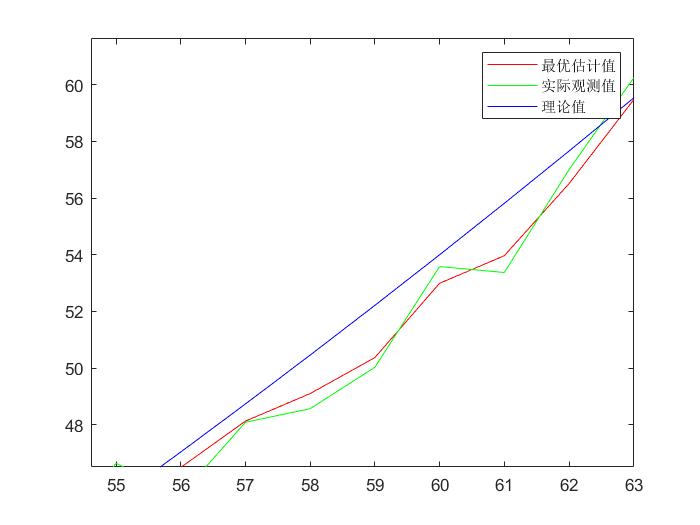
实例：小车匀加速运动

我们将上面所述的实例代码如下：

% 说明
% 模型：匀加速运动
% x_optimal 最优估计值
% x_observe 观测值
% x_predict 先验估计值（预测值）

total = 300;
delta = 0.1;
x_observe(1) = 0;
w = randn(1, total);
Q = (std(w)).^2;
v = randn(1, total);
R = (std(v)).^2;
a = 3;
for n = 2:total
    REF(n) = 1/2*a*(n*delta).^2;
    x_observe(n) = x_observe(n-1) + a*(n-1/2)*delta.^2  + w(n);
    y(n) = x_observe(n) + v(n);
end

p_observe(1) = 1;  
x_optimal(1) = 0;  
for n = 2:total
    % 预测
    x_predict(n) = x_optimal(n-1) + a*(n-1/2)*delta.^2;
    p_predict(n) = p_observe(n-1) + Q;
    % 更新
    k(n) = p_predict(n) / (p_predict(n) + R);
    x_optimal(n) = x_predict(n) + k(n) * (y(n) - x_predict(n))
    p_observe(n) = (1 - k(n))*p_predict(n); 
end

n = 1:total;
plot(n, x_optimal, 'r', n ,y, 'g', n, REF, 'b');
legend('最优估计值', '实际观测值', "理论值")

结果如下：